A fejlődés logisztikus modellje
A képességek fejlődésében alapvetően kétféle mintázatot különböztethettünk meg. Egy lassuló-gyorsuló-lassuló lefutású folyamatot, és egy ettől eltérő, több gyors és lassú szakaszból álló fejlődésmenetet.
Bizonyos feltételek fennállása esetén a logisztikus függvény jól írja le a képességek fejlődését is. A képességek fejlettségének logisztikus változására számíthatunk abban az esetekben, amikor a képesség időegységre eső fejlettsége arányos magának a képességnek az aktuális fejlettségi szintjével. Ez a feltétel tulajdonképpen minden képesség esetében fennáll, hiszen a képesség fejlettebb szintjén többet lehet gyakorolni magát a képességet, már csak azért is, mert fejlettebb képességgel időegység alatt több gyakorlatot lehet elvégezni, mint a kevésbé fejlett szinten. A korlát létezését szükségtelen bizonyítani, a biológiai korlátok, az információ-feldolgozó kapacitás mindenfajta megismerő tevékenysége számára jelentenek egy végső korlátot.
Logisztikus görbe illesztése a mért adatokhoz
Ahhoz, hogy a mért adatok pontosan "kirajzolják" a fejlődés valódi sajátosságait, sok mérési pontra, széles életkori sávot, a fejlődés teljes szakaszát lefedő eredményekre van szükség. A logisztikus görbe alakjából következően legalább öt "jól eltalált" időpontban kell mérési adattal rendelkeznünk ahhoz, hogy a görbe alakja egyértelműen kirajzolódjon. Kell egy adat a fejlődési folyamat első, még lassú és az utolsó, már lassú szakaszáról, továbbá a gyors középső szakaszról. Ha három pontunk van, azokat egyenes szakaszokkal éppen úgy összeköthetjük. mint sok más egyéb görbével. Ha a középső és a szélső pontok között van még egy-egy adatunk, az már egyértelműbben jelezheti a logisztikus jelleget.
Az arány feladat megoldásának változása az életkor függvényében egy szabályos logisztikus fejlődésre utal. A mért adatokat és az azokhoz illesztett logisztikus görbét a 12. ábra mutatja be.
Az illesztés automatikus, többnyire a legkisebb négyzetek elvével meghatározza a program a mért adatokhoz legközelebb álló függvény paramétereit. Ez a megoldás objektív abban az értelemben, hogy az eredmény nem tartalmaz egyéb feltevéseket vagy elvárásokat, és érdemes is megvizsgálni, mire megy a program az adatainkkal, ha "magára hagyjuk". A gyakorlatban azonban jobb eredményre jutunk, ha a függvényt egyedi számításokkal határozzuk meg, és többféle megoldással próbálkozunk.
A 12. ábrán bemutatott megoldás esetében a logisztikus görbe nagy pontossággal illeszkedik a mért adatokra. Mivel a görbét az iskolai oktatás életkori határain túl is megrajzoltuk, a vízszintes tengelyen az időt az életkorral jellemeztük. A mért és a számított adatok különbsége alig néhány százalékos, és az ábrán szereplő függvény egyik mérési pontra sem illeszkedik pontosan. Látható azonban, hogy legjobban a tizenegy évesek (ötödik évfolyam) adata tér el - mégpedig felfele - a számított értéktől.
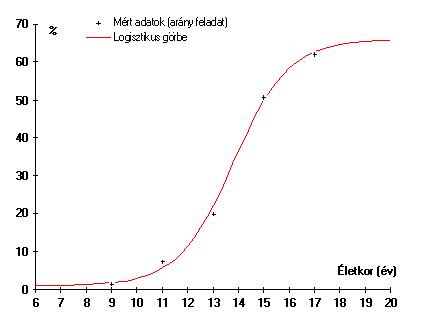
12. ábra. Az arány feladatot megoldók százalékban a mért adatokhoz illesztett logisztikus görbével
Elvégeztük a logisztikus görbe illesztését az induktív gondolkodás fejlettségét leíró adatokhoz
is (l. 13. ábra).
Annak érdekében, hogy a teszt sajátosságait (a találgatás valószínűségét) is figyelembe vegyük,
itt a logisztikus függvény korábban bemutatott formáját egy a konstanssal egészítettük ki.
A konstans azt fejezi ki, hogy a képesség "0 fejlettségéhez" nem 0 tesztpontszám tartozik,
hiszen valamennyi pontot a feleletválasztós teszteken véletlen találgatással is el lehet érni.
Az ábra jól szemlélteti az induktív gondolkodás fejlődésének szabályos jellegét. Itt már nem tapasztaltunk olyan eltéréseket, felgyorsuló vagy lassuló szakaszokat, ami az iskolai oktatás hatásának lenne tulajdonítható.
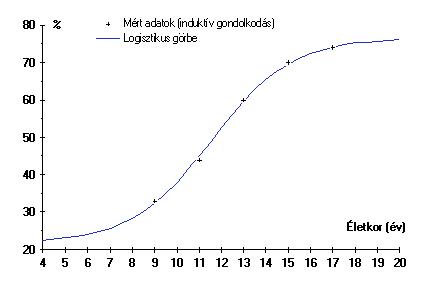
13. ábra. Az induktív gondolkodás fejlettsége az életkor függvényében a mért adatokhoz illesztett logisztikus görbével

